Blog

Jesteś początkującym w świecie informatyki? Chcesz lepiej zrozumieć działanie systemu binarnego, ale nie masz pojęcia, jak dodawać liczby w tym systemie? Spokojnie, nie ma co panikować! W tym artykule przeprowadzę Cię krok po kroku przez podstawy systemu binarnego i pokażę, jak wykonywać w nim zamianę systemu dziesiętnego na binarny, oraz działanie dodawania liczb w systemie dwójkowym. Nie będzie to wcale takie trudne, jak myślisz! Zacznę od wyjaśnienia, czym w ogóle jest system binarny i jak działają w nim operacje arytmetyczne. Następnie przejdę do sedna – dodawania liczb binarnych. Zilustruję to kilkoma przykładami krok po kroku, żebyś dobrze zrozumiał zasadę. Na koniec znajdziesz proste ćwiczenia z rozwiązaniami, dzięki którym szybko opanujesz tę umiejętność. Więc zaczynamy!

Podział Systemów Liczbowych – Wprowadzenie

Systemy nie pozycyjne

W matematyce istnieje wiele systemów liczbowych, z których niektóre są pozycyjne, a inne nie. Przykładem systemu liczbowego nieopartego na pozycji jest system rzymski. W tym systemie liczby są reprezentowane przez symbole, takie jak I, V, X, L, C, D i M. Wartość każdego symbolu jest stała, niezależnie od jego położenia.

System dziesiętny

Najbardziej znanym systemem liczbowym jest system dziesiętny, w którym do zapisu liczb używamy 10 cyfr (0, 1, 2, 3, 4, 5, 6, 7, 8, 9). Jest to system pozycyjny, ponieważ wartość każdej cyfry zależy od jej położenia. Na przykład liczba 234 oznacza 2 x 100 + 3 x 10 + 4 x 1.

System binarny

Innym ważnym systemem liczbowym jest system binarny. Jest to system dwójkowy, w którym do zapisu liczb używa się tylko dwóch cyfr: 0 i 1. Podobnie jak w systemie dziesiętnym, system binarny jest systemem pozycyjnym. Na przykład liczba 1010 oznacza 1 x 8 + 0 x 4 + 1 x 2 + 0 x 1, czyli 8 + 0 + 2 + 0 = 10.

System binarny jest szczególnie ważny w informatyce, ponieważ komputery przechowują i przetwarzają informacje w postaci liczb binarnych. Znajomość systemu binarnego i umiejętność wykonywania w nim działań arytmetycznych, takich jak dodawanie i odejmowanie, jest przydatna dla każdego, kto chce zrozumieć, jak działają komputery.

System Binarny – Na Czym Polega?

System binarny, znany również jako system dwójkowy, to sposób zapisywania liczb za pomocą tylko dwóch cyfr: 0 i 1. Liczby są reprezentowane przez ciągi zer i jedynek o określonej długości. Każda pozycja w ciągu ma wartość mocy dwójki, licząc od prawej do lewej.

Zasada działania

W systemie binarnym 1 = 1, 10 = 2, 11 = 3, 100 = 4 i tak dalej.

Aby przeliczyć liczbę binarną na dziesiętną, należy pomnożyć każdą cyfrę (0 lub 1) przez odpowiednią wartość potęgi dwójki i zsumować wyniki. Numerację potęg zaczynamy od prawej strony zawsze od 0.

Na przykład:

101 = 1 x 2^2 + 0 x 2^1 + 1 x 2^0 = 4 + 0 + 1 = 5

Zastosowanie systemu dwójkowego

System binarny jest powszechnie stosowany w informatyce i elektronice. Komputery przechowują dane i wykonują obliczenia w postaci ciągów zer i jedynek. Prawie wszystkie informacje cyfrowe, takie jak tekst, obrazy, muzyka i wideo, są kodowane w systemie binarnym. System binarny jest również używany do reprezentowania liczb w układach scalonych, takich jak mikroprocesory.

Zamiana systemu dziesiętnego na binarny

Przypomnijmy sobie system dziesiętny

System dziesiętny, z którym na co dzień mamy do czynienia, używa 10 cyfr – od 0 do 9. Każda kolejna cyfra w liczbie ma wartość dziesięciokrotnie większą od poprzedniej, licząc od prawej do lewej. Na przykład liczba 256 zapisana w systemie dziesiętnym oznacza: 6 x 1 + 5 x 10 + 2 x 100 = 256.

Zamiana na system dwójkowy (binarny)

W systemie binarnym używane są tylko dwie cyfry: 0 i 1. Tutaj każda kolejna cyfra ma wartość dwukrotnie większą od poprzedniej, licząc od prawej do lewej. Na przykład liczba 256 w systemie binarnym zapiszemy jako: 1 x 128 + 1 x 64 + 0 x 32 + 0 x 16 + 0 x 8 + 1 x 4 + 1 x 2 + 0 x 1 = 256.

Krok po kroku

Aby przekonwertować liczbę z systemu dziesiętnego na binarny, wykonaj następujące kroki:

1. Podziel liczbę przez 2. Zapisz resztę jako ostatnią cyfrę wyniku w systemie binarnym.
2. Ponownie podziel resztę przez 2. Zapisz nową resztę jako kolejną cyfrę wyniku.
3. Powtarzaj krok 2 dopóki reszta nie będzie równa 0.
4. Odczytaj wynik w systemie binarnym od końca.

Przykład

Przekonwertujmy liczbę 13 na system binarny:

1. 13 / 2 = 6, reszta 1. Zapisz 1 jako ostatnią cyfrę.
2. 6 / 2 = 3, reszta 0. Zapisz 0.
3. 3 / 2 = 1, reszta 1. Zapisz 1.
4. 1 / 2 = 0, reszta 1. Zapisz 1.

Wynik w systemie binarnym: 1101.

Instrukcja jak zamieniać liczby z systemu dziesiętnego na binarny

Zanotuj liczbę w systemie dziesiętnym

Zanim przejdziesz do zamiany liczby na system binarny, zanotuj liczbę w systemie dziesiętnym. Na przykład możesz wybrać liczbę 47.

Podziel liczbę przez 2

Podziel podaną liczbę przez 2. W naszym przykładzie 47 podzielone przez 2 daje 23 reszta 1. Zapisz resztę, która będzie pierwszą cyfrą w systemie binarnym.

Kontynuuj dzielenie przez 2

Teraz podziel resztę 23 przez 2. Otrzymasz 11 reszta 1. Ponownie zapisz resztę jako kolejną cyfrę w systemie binarnym.

Powtarzaj do uzyskania reszty 0

Kontynuuj dzielenie przez 2 i zapisywanie reszt aż do uzyskania reszty 0. W naszym przykładzie:

11 / 2 = 5 reszta 1 5 / 2 = 2 reszta 1 2 / 2 = 1 reszta 0

Odczytaj liczbę binarną od dołu do góry

Teraz odczytaj liczbę binarną od dołu do góry: 1 1 0 1. W systemie dziesiętnym jest to 47.

Gratulacje! Umiesz teraz zamieniać liczby dziesiętne na binarne. Ćwicz tę umiejętność rozwiązując więcej przykładów. Pamiętaj, że im więcej ćwiczysz, tym lepiej opanujesz zamianę pomiędzy systemami liczbowymi!

Ćwiczenia z zamiany systemu dziesiętnego na binarny

Ćwiczenie 1

Zamień liczbę dziesiętną 15 na binarną:

1. Dziel 15 przez 2. Reszta z dzielenia to 1, a iloraz to 7.
2. Dziel 7 przez 2. Reszta to 1, a iloraz to 3.
3. Dziel 3 przez 2. Reszta to 1, a iloraz to 1.
4. 1 podzielone przez 2 daje 0 z resztą 1.
5. Odczytujemy liczbę binarną od dołu do góry: 1111.

Czyli, 15 w systemie binarnym to 1111.

Ćwiczenie 2

Zamień liczbę dziesiętną 47 na binarną:

1. 47 podzielone przez 2 daje resztę 1 i iloraz 23.
2. 23 podzielone przez 2 daje resztę 1 i iloraz 11.
3. 11 podzielone przez 2 daje resztę 1 i iloraz 5.
4. 5 podzielone przez 2 daje resztę 1 i iloraz 2.
5. 2 podzielone przez 2 daje resztę 0 i iloraz 1.
6. 1 podzielone przez 2 daje resztę 1 i iloraz 0.
7. Odczytujemy liczbę binarną od dołu do góry: 101111.

Czyli, 47 w systemie binarnym to 101111.

Ćwiczenie 3

Zamień liczbę dziesiętną 129 na binarną:

1. 129 podzielone przez 2 daje resztę 1 i iloraz 64.
2. 64 podzielone przez 2 daje resztę 0 i iloraz 32.
3. 32 podzielone przez 2 daje resztę 0 i iloraz 16.
4. 16 podzielone przez 2 daje resztę 0 i iloraz 8.
5. 8 podzielone przez 2 daje resztę 0 i iloraz 4.
6. 4 podzielone przez 2 daje resztę 0 i iloraz 2.
7. 2 podzielone przez 2 daje resztę 0 i iloraz 1.
8. 1 podzielone przez 2 daje

Ćwiczenia

Wykonaj następujące zadania, aby przećwiczyć dodawanie w systemie dwójkowym:

1. 1010 + 0111 = ? Rozwiązanie: 1010 = 12^3 + 02^2 + 12^1 + 02^0 = 8 + 0 + 2 + 0 = 10 0111 = 02^3 + 12^2 + 12^1 + 12^0 = 0 + 4 + 2 + 1 = 7 1010 + 0111 = 10 + 7 = 17 = 12^4 + 02^3 + 02^2 + 12^1 + 1*

Dodawanie W Systemie Binarnym – Krok Po Kroku

Zamień liczby na system binarny

Aby dodać dwie liczby w systemie binarnym, musisz najpierw zamienić je na postać binarną. Na przykład, liczba 5 w systemie dziesiętnym to 0101 w systemie binarnym, a liczba 7 to 0111. Zapisz obie liczby w kolumnie, przesuwając mniej znaczące cyfry w prawo.

Wyrównaj liczby i dodaj od prawej do lewej

Teraz wyrównaj obie liczby przez dodanie zer wiodących. Na przykład:

5 (0101) 7 (0111)

Teraz obie liczby mają taką samą długość i można je dodać. Zacznij od kolumny o najmniejszej wadze po prawej stronie. 0 + 1 = 1. Zapisz 1 pod spodem i przenieś 1 do następnej kolumny. 1 + 1 + przeniesione 1 = 3. Ponieważ maksymalna cyfra w systemie binarnym to 1, zapisz 1 i przenieś 1 do następnej kolumny. 0 + 0 + przeniesione 1 = 1.

Wynik końcowy to 1010, co w systemie dziesiętnym odpowiada liczbie 10. Ćwicz tę procedurę kilkakrotnie, aby przyzwyczaić się do dodawania w systemie binarnym.

Działanie	Wynik	Uwagi
0+0	0	Analogicznie jak w systemie dziesiętnym
0+1	1	Analogicznie jak w systemie dziesiętnym
1+0	1	Analogicznie jak w systemie dziesiętnym
1+1	1 | 0	0 z przeniesieniem Przeniesienie to konieczność dodania jedynki do następnej kolumny
1+1+1	1 | 1	1 z przeniesieniem Przeniesienie to konieczność dodania jedynki do następnej kolumny

Dodawanie liczb binarnych krok po kroku:

1. Sumowane liczby zapisujemy jedna pod drugą tak, aby w kolejnych kolumnach znalazły się cyfry stojące na pozycjach o tych samych wagach

2. Sumowanie rozpoczynamy od ostatniej kolumny. Sumujemy cyfry w kolumnie zgodnie z podaną tabelką zapisując wynik pod kreską:

3. Jeśli wynik sumowania jest dwucyfrowy (1 + 1 = 10), to pod kreską zapisujemy tylko ostatnią cyfrę 0, a 1 przechodzi do następnej kolumny

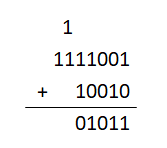
5.Jeśli w krótszej liczbie zabrakło cyfr, to dopisujemy zera. Pamiętajmy o przeniesieniach

1. Dodaliśmy wszystkie cyfry, ale przeniesienie wciąż wynosi 1. Zatem dopisujemy je do otrzymanego wyniku

1111001₍₂₎ + 10010₍₂₎ = 10001011₍₂₎

121 + 18 = 139

Korzystaj z arkusza kalkulacyjnego, aby ułatwić obliczenia

Możesz stworzyć prosty arkusz kalkulacyjny, aby pomóc Ci w dodawaniu liczb binarnych. Narysuj dwie kolumny dla dwóch liczb i kolumnę dla wyniku. Wpisz liczby binarne w pierwszych dwóch kolumnach, a następnie dodaj od prawej do lewej, zapisując wyniki w kolumnie wyniku i przenosząc, jeśli wynik kolumny jest większy niż 1. Ten prosty arkusz kalkulacyjny pomoże Ci

Przykłady Dodawania Liczb Binarnych

Dodawanie dwóch liczb jednocyfrowych

Aby dodać dwie liczby jednocyfrowe w systemie binarnym, po prostu dodaj cyfry. Na przykład:

0 + 0 = 0 0 + 1 = 1 1 + 0 = 1 1 + 1 = 10 (w systemie dziesiętnym to 2, ale w binarnym zapisujemy to jako 10)

Dodawanie liczb wielocyfrowych

Gdy dodajesz liczby wielocyfrowe, dodaj cyfry jednostek, a następnie przenieś jedynkę, jeśli wynik jest 10 lub więcej. Na przykład:

10 + 01 = 11 101 + 011 = 1000 1 + 1010 = 1011

Dodawanie liczb o różnej liczbie cyfr

Jeśli dodajesz liczby o różnej liczbie cyfr, wyrównaj liczby dodając zera wiodące do krótszej liczby. Na przykład:

10 + 101 = 111 010 + 101 = 111 101 + 0101 = 1000

Kilka przykładów

Oto kilka przykładów dodawania liczb binarnych:

1 + 1 = 10 10 + 10 = 100 11 + 11 = 110 101 + 010 = 111 1001 + 0111 = 10110

Dodawanie liczb binarnych jest dość proste, jeśli pamiętasz, aby zawsze zaczynać od kolumny jednostek, przenosić jedynkę, gdy wynik jest 10 lub więcej i wyrównywać liczby dodając wiodące zera. Ćwicz z kilkoma przykładami, a szybko opanujesz sztukę dodawania w systemie binarnym!

Ćwiczenia – Jak Dodać Liczby Binarne? (Z Rozwiązaniami)

Dodawanie dwóch liczb binarnych o tej samej długości

Najpierw należy wyrównać liczby, umieszczając mniej znaczące cyfry po lewej stronie. Następnie dodaj cyfry na tych samych pozycjach, zaczynając od najmniej znaczących cyfr. Jeśli wynik jest większy niż 1, zapamiętaj go i przenieś 1 do kolejnej pozycji. Powtarzaj, aż dojdziesz do najbardziej znaczącej cyfry.

Na przykład:

11 (binarnie: 1011) +10 (binarnie: 1010)

Wyrównaj liczby:

1011 +1010

---

Dodaj cyfry:

1 + 0 = 1 Przenieś 1 0 + 1 = 1
1 + 0 = 1 1 + 1 = 2 (zapamiętaj 1, przenieś 1)

Ostateczny wynik:

21 (binarnie: 10101)

Ćwiczenie

Dodaj następujące liczby binarne:

1. 1101 +1011

---

Rozwiązanie: 1101 +1011

---

10110

2. 10011 +11101

---

Rozwiązanie: 10011 +11101

---

22100

3. 11100 +11000

---

Rozwiązanie: 11100 +11000

---

101100

4. 11111 +11111

---

Rozwiązanie: 11111 +11111

---

11110

Jak widać, dodawanie liczb binarnych jest proste, kiedy zna się kroki. Ćwicz codziennie, aby opanować tę ważną umiejętność w dziedzinie informatyki!

Aby mieć pewność, że prawidłowo dokonałeś zamiany systemów liczbowych, czy też dodawania w systemie binarnym, możesz skorzystać z kalkulatora systemowego. Uruchom kalkulator -> kliknij menu (3 kreseczki) wybierz tryb programisty:

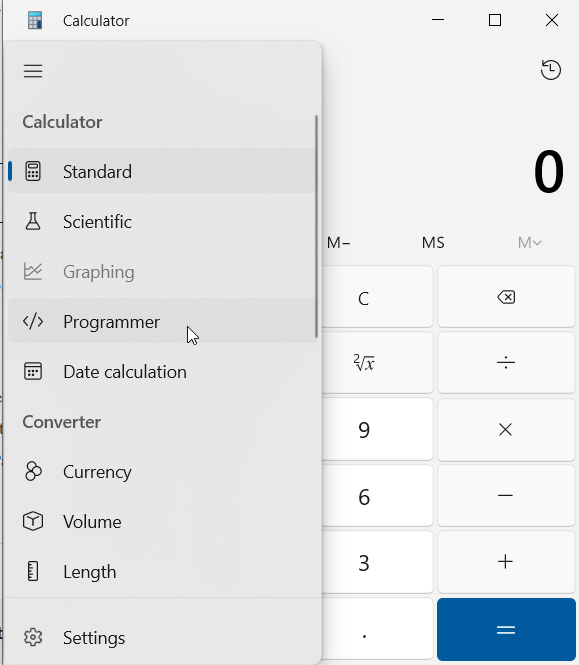
Następnie wybierz który system Cię interesuje i wykonuj obliczenia sprawdzające. Pamiętaj HEX – oznacza system szesnastkowy, DEC – system dziesiętny, OCT – system ósemkowy, BIN – system binarny.

Podsumowanie

No i to by było na tyle, jeśli chodzi o dodawanie liczb binarnych! Mam nadzieję, że ten przewodnik z przykładami i ćwiczeniami pokazał Ci krok po kroku, jak sobie radzić z tym zadaniem. Dodawanie w systemie dwójkowym może wydawać się skomplikowane na początku, ale z praktyką na pewno sobie poradzisz. Pamiętaj tylko o przenoszeniu jedynki i sprawdzaniu wyniku. Jeśli masz jakieś pytania lub wątpliwości, koniecznie daj znać w komentarzu. Trzymam kciuki, żebyś bez problemu opanował tę umiejętność!